#
Dr. M. Baron, Statistical Machine Learning class, STAT-427/627
# CLUSTERING
0.
Review of principal components –
another unsupervised learning method
> attach(USArrests)
This data set contains statistics, in arrests per 100,000 residents
for assault, murder, and rape in each of the 50 US states in 1973. Also given
is the percent of the population living in urban
areas.
> names(USArrests)
[1] "Murder" "Assault" "UrbanPop"
"Rape"
> pc = prcomp(USArrests, scale=TRUE)
> biplot(pc)
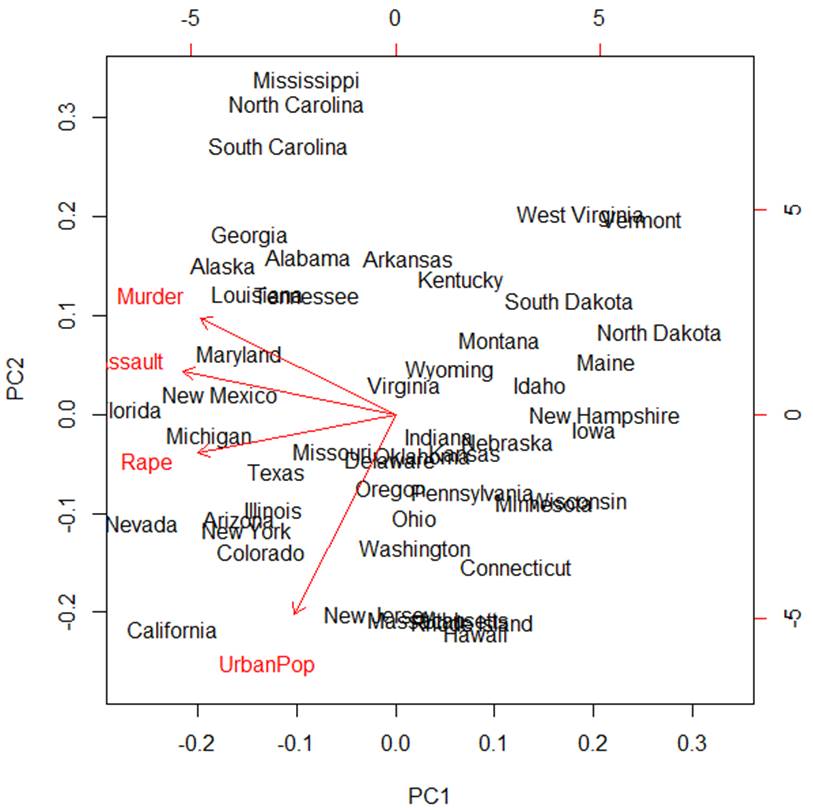
Red vectors are projections of the original X-variables on the space
of the first two principal components. We can see that the first principal
component Z1 mostly represents the combined crime rate, and the
second principal component Z2 mostly represents the level of
urbanization.
1. K-means method
Now we use K-means clustering to find more homogeneous groups among
the states.
Let’s start with K=2 clusters. The 50 states are partitioned into 2
groups, Cluster 1 with 21 and Cluster 2 with 29 states.
> KM2 = kmeans(X,2)
> KM2
K-means clustering with 2 clusters of sizes 21,
29
Cluster means:
Murder Assault UrbanPop Rape
1 11.857143 255.0000 67.61905 28.11429
2
4.841379 109.7586 64.03448 16.24828
Clustering vector:
Alabama Alaska Arizona Arkansas California
1 1 1 1 1
Colorado Connecticut Delaware Florida Georgia
1 2 1 1 1
Hawaii Idaho Illinois Indiana Iowa
2 2 1 2 2
Kansas Kentucky Louisiana Maine Maryland
2 2 1 2 1
Massachusetts Michigan Minnesota Mississippi Missouri
2 1 2 1 2
Montana Nebraska Nevada
New Hampshire New Jersey
2 2 1 2 2
New
Mexico New York North Carolina North Dakota Ohio
1 1 1 2 2
Oklahoma Oregon Pennsylvania Rhode Island South Carolina
2 2 2 2 1
South
Dakota Tennessee Texas Utah Vermont
2 1 1 2 2
Virginia Washington West Virginia Wisconsin Wyoming
2 2 2 2 2
Within cluster sum of squares by cluster:
[1] 41636.73 54762.30
(between_SS / total_SS = 72.9 %)
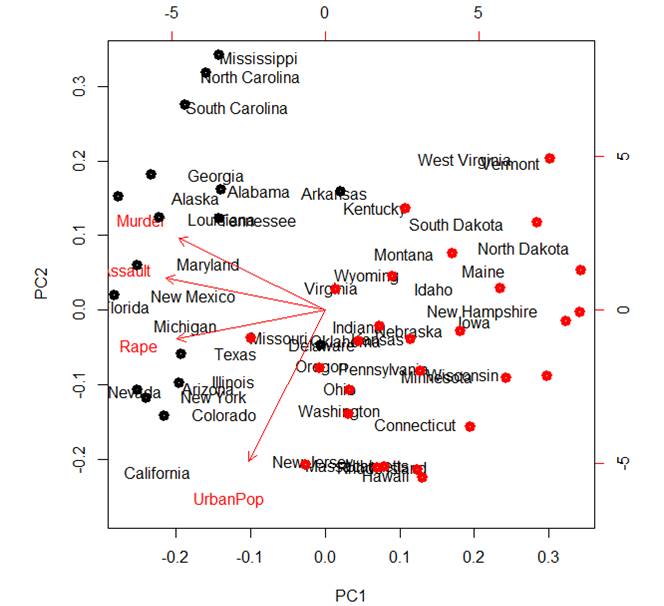
Let’s look at the position of these clusters on our biplot. There is
a discrepancy of scales in biplot, so I am using a coefficient 3.5, to match
points to state names.
> points(3.5*pc$x[,1],
3.5*pc$x[,2], col=KM2$cluster, lwd=5)
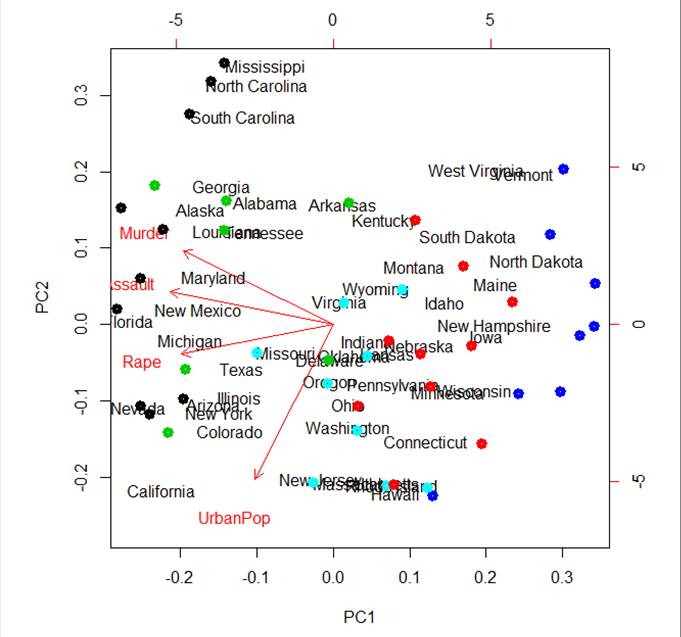
Use more clusters?
> KM5 = kmeans(X,5)
> points(3.5*pc$x[,1],
3.5*pc$x[,2], col=KM5$cluster, lwd=5)
2. Hierarchical Clustering and Dendrogram
So, how many clusters should be used? We can apply the hierarchical
clustering algorithm, which does not require to
pre-specify the number of clusters.
> HC = hclust( dist(X),
method="complete" )
Here, “dist” stays for distance between
multivariate observations, and method can be “complete”, “single”, “average”,
“median”, etc. – it is a method of determining similarity with clusters and
dissimilarity between clusters.
We can see the dendrogram that
this method has created.
> plot(HC)
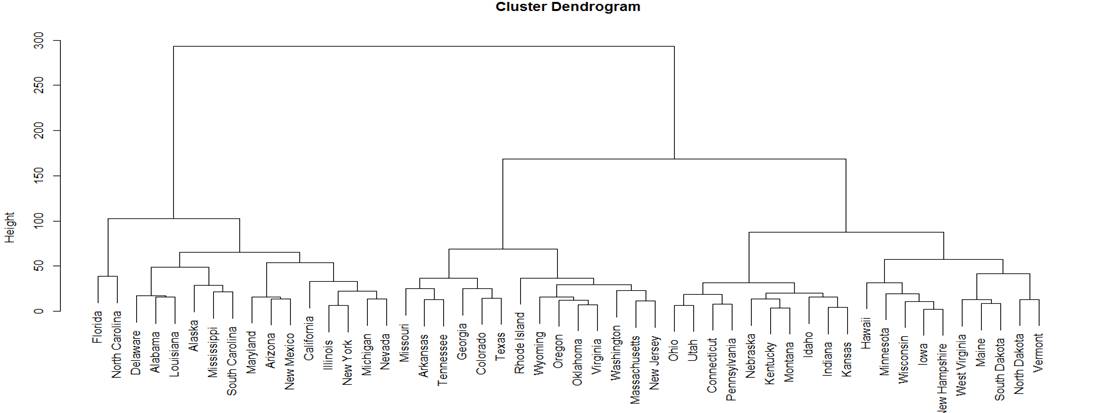
We then cut the tree at some level and create clusters.
> cutree(HC,5)
Alabama Alaska Arizona Arkansas California
1 1 1 2 1
Colorado Connecticut Delaware Florida Georgia
2 3 1 4 2
Hawaii Idaho Illinois Indiana Iowa
5 3 1 3 5
Kansas Kentucky Louisiana Maine Maryland
3 3 1 5 1
Massachusetts Michigan Minnesota Mississippi Missouri
2 1 5 1 2
Montana Nebraska Nevada
New Hampshire New Jersey
3 3 1 5 2
New
Mexico New York North Carolina North Dakota Ohio
1 1 4 5 3
Oklahoma Oregon Pennsylvania Rhode Island South Carolina
2 2 3 2 1
South
Dakota Tennessee Texas Utah Vermont
5 2 2 3 5
Virginia Washington West Virginia Wisconsin Wyoming
2 2 5 5 2
3. College data - K-means method
Our task will be to cluster Colleges into more homogeneous groups.
> attach(College); names(College)
[1] "Private" "Apps" "Accept" "Enroll" "Top10perc" "Top25perc" "F.Undergrad"
"P.Undergrad" "Outstate" "Room.Board"
[11] "Books" "Personal" "PhD" "Terminal" "S.F.Ratio" "perc.alumni"
"Expend" "Grad.Rate"
We need to create a matrix of numeric variables. We’ve used this
command to prepare data for LASSO.
> X = model.matrix(
Private ~ . + as.numeric(Private), data=College )
> dim(X)
[1] 777
19
> head(X) Instead of printing the entire matrix,
“head” only shows the first few rows
(Intercept) Apps
Accept Enroll Top10perc Top25perc F.Undergrad P.Undergrad Outstate Room.Board
Books Personal PhD
Abilene
Christian University 1
1660 1232 721
23 52 2885 537
7440 3300 450
2200 70
Adelphi
University 1
2186 1924 512
16 29 2683 1227
12280 6450 750
1500 29
Adrian
College 1 1428
1097 336 22 50 1036 99
11250 3750 400
1165 53
Agnes
Scott College 1 417
349 137 60 89 510 63
12960 5450 450
875 92
Alaska
Pacific University 1 193
146 55 16 44 249 869
7560 4120 800
1500 76
Albertson
College 1 587
479 158 38 62 678 41
13500 3335 500
675 67
Terminal S.F.Ratio perc.alumni Expend Grad.Rate as.numeric(Private)
Abilene
Christian University 78 18.1 12
7041 60 2
Adelphi
University 30 12.2 16
10527 56 2
Adrian
College 66 12.9 30
8735 54 2
Agnes
Scott College 97 7.7 37
19016 59 2
Alaska
Pacific University 72 11.9 2
10922 15 2
Albertson
College 73 9.4 11
9727 55 2
Now, let’s create K=5 clusters by the K-means method. No new library
is needed, this command comes with basic R.
> KM5 = kmeans( X, 5 )
> KM5
K-means
clustering with 5 clusters of sizes 20, 113, 162, 431, 51
Cluster
means:
(Intercept) Apps
Accept Enroll Top10perc
Top25perc F.Undergrad P.Undergrad Outstate Room.Board Books Personal PhD Terminal
1 1
9341.750 3606.2500 1321.9500
76.05000 91.70000 5283.200
427.2000 18119.750 6042.750
576.6000 1255.550 93.30000 96.80000
2 1
5012.602 3410.1150 1526.5310
21.56637 52.28319 8021.566
2111.3097 6709.283 3703.912 557.1416 1727.186 77.01770 83.65487
3 1
2566.364 1712.7901 521.5123 39.83333
68.96914 2067.241 282.4444 15732.512 5257.864 578.0926 1042.772 83.31481 90.24074
4 1
1140.610 869.9258 341.7007
21.40371 48.75638 1434.332
475.6450 9263.759 4110.290 530.1206 1299.220 65.03016 72.61717
5 1 13169.804 8994.7647 3438.1176 34.84314
67.15686 17836.020 3268.3529
8833.510 4374.353 593.0784
1813.784 85.54902 90.64706
S.F.Ratio perc.alumni Expend
Grad.Rate as.numeric(Private)
1 6.61500
35.35000 32347.900 88.95000 2.000000
2 17.46903
14.02655 7067.257 54.91150 1.079646
3 11.43333
32.76543 13728.735 76.64198 1.993827
4 14.32343
21.36659 7677.035 63.13225 1.856148
5 15.99608
16.92157 10343.882 63.82353 1.117647
Clustering
vector:
Abilene Christian
University
Adelphi University Adrian College
4
3 4
Agnes Scott
College Alaska
Pacific University
Albertson College
3
4 4
Albertus Magnus
College
Albion College Albright College
4
3 3
Alderson-Broaddus
College
Alfred University Allegheny College
4
3 3
<truncated>
Within
cluster sum of squares by cluster:
[1]
2115931982 3262290091 3917614114 5524699694 5934672728
(between_SS / total_SS = 71.2 %)
Available
components:
[1]
"cluster"
"centers" "totss"
"withinss" "tot.withinss"
"betweenss" "size" "iter" "ifault"
We can see the cluster assignment (truncated), multivariate cluster
means (centroids), within and between sums of squares as measures of cluster
purity. To explore the obtained clusters, we can plot some pairs of variables
along with the assigned clusters:
> par(mfrow=c(2,2))
> plot( Outstate, Top10perc, col=KM5$cluster
)
> plot( S.F.Ratio,
PhD, col=KM5$cluster )
> plot( Apps, Enroll, col=KM5$cluster )
> plot( Room.Board,
Private, col=KM5$cluster )

For example, we can see here that the green cluster consists of
rather expensive and relatively small private colleges with a high percent of PhD degrees among faculty and small class sizes
because of a low student-to-faculty ratio.
4. College data - Hierarchical Clustering
Without specifying the number K of clusters, apply hierarchical
clustering algorithm to the College data.
> HC = hclust( dist(X),
method="complete" )
Here, “dist” stays
for distance between multivariate observations, and method can be “complete”,
“single”, “average”, “median”, etc. – it is a method of determining similarity
with clusters and dissimilarity between clusters.
The full dendrogram with so
many leafs would not be legible.
> plot(HC)
To illustrate the method, let’s take a small random sample of
colleges and cluster them hierarchically.
> Z = sample(n,20)
> Y = X[Z,]
> HCZ = hclust( dist(Y), method="complete" )
> plot(HCZ)
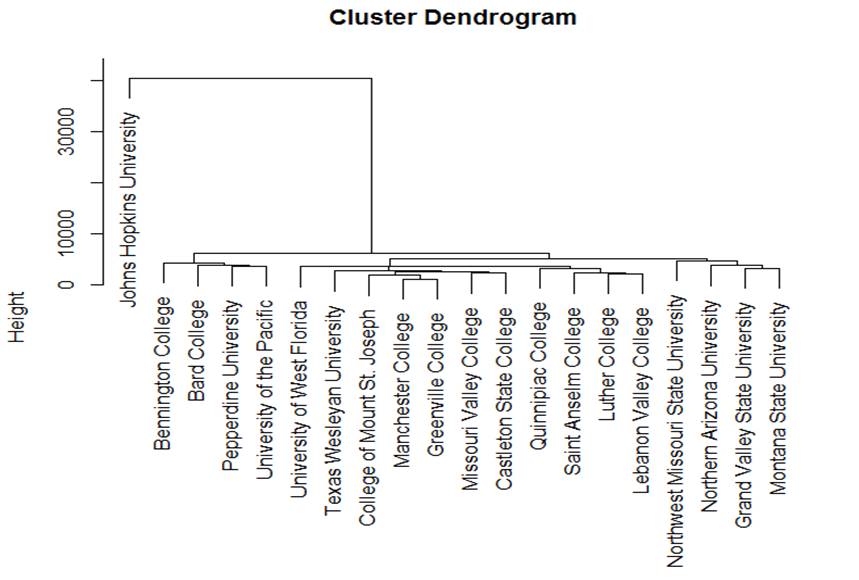
We can choose where to “cut” this tree to create clusters. For
example, we let’s create 4 clusters.
> HC4 = cutree(HC, k = 4)
> HC4
Christian Brothers University
Nazareth College of Rochester
1 1
Sweet Briar College
Dartmouth College
1 2
Eckerd College Appalachian State University
1 3
< truncated >
So, we get assignments of colleges into clusters.